最近在練習Kaggle，使用到許多沒使用過的機器學習的方法，尤其在回歸問題上，遇到了LinearRegression、Ridge、Lasso、GradientBoostingRegressor、ExtraTreesRegressor、SVR、ElasticNet、SGDRegressor、 BayesianRidge、KernelRidge、XGBRegressor等等，對我個人而言有些方法名稱是與分類問題類似的，像是SVR、BayesianRidge、XGBRegressor等等，另外Ridge和Lasso查資料才發現它其實就是最小二乘數+正則化，那正則化和其它許許多多的方法未來有時間會仔細的研讀在做相關的筆記，本次主要介紹Support Vector Machine(SVM)中的分類技巧，也就是所為Support Vector Classification(SVC)。
這次主要筆記林軒田教授的機器學習技法，筆記的內容主要是結合林軒田教授的說法與自己的想法去解釋並且實作，另外在機器學習上面，除了林軒田老師的貢獻外，台灣還有許多人也都在默默的貢獻教學文章，這次主要舉例有介紹SVM部分的兩人，Tommy Huang和Fukuball，Tommy Huang介紹的機器學習和深度學習都使用詳細的推導來去說明，但有些推導是建立在一些先備知識上，所以若要理解有時候必須中途去補足缺少的知識;Fukuball則是主要實作有關林軒田教授介紹的機器學習方法，並且開發出名為FukuML的套件，我認為FukuML是一個簡顯易懂的套件，主要做研究時能容易使用，畢竟在研究時必須知道方法的特性才能加以運用或改進，當然不只他們在中文這部分做出貢獻，在此要感謝辛苦在中文語言這塊持續貢獻的人。
因為剛好用到Kernel和SVM所以直接看機器學習技法，但若基礎不好或者要仔細的學建議從機器學習基石開始，因為若不熟悉一些基本觀看機器學習技法可能會有些名詞或一些技巧不太懂，但也可以看不懂再查就好，最終還是看個人的學習方法，畢竟沒人敢保證從哪裡開始學能有最大效益。
此筆記主要的目標是，結合實作和林軒田教授的講解與自己的想法，進而學習到SVM的精隨，在未來上遇到類似的問題都能夠加以運用。另外若需要完整的學習能去觀看林軒田教授的機器學習技法。
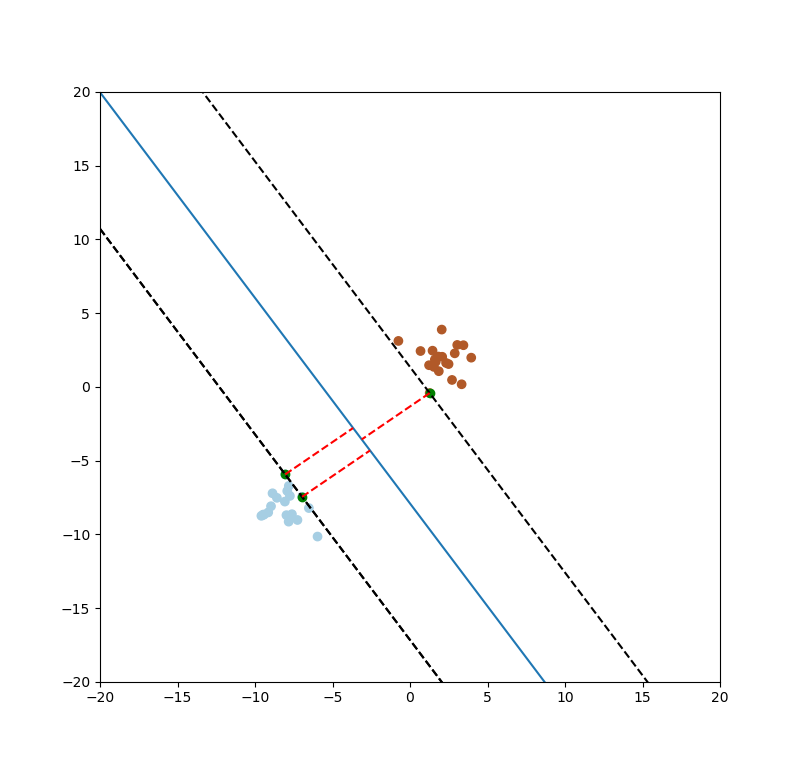
SVM的目的要找出最大的間距(margin)，如下圖一紅色線條。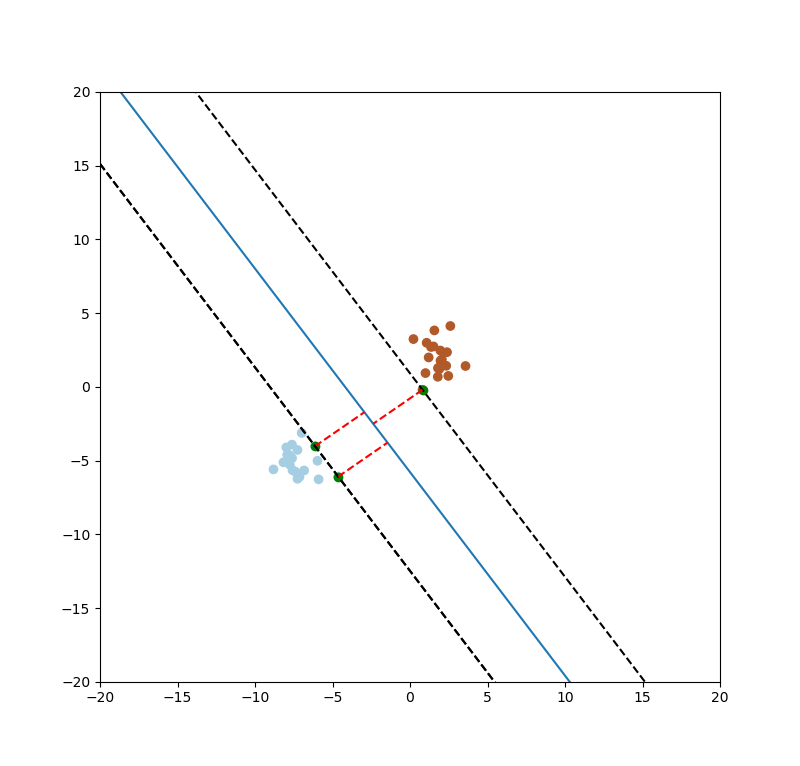
圖一。
要如何找到最大的margin?首先將圖一的藍色線條轉為一個線性方程式為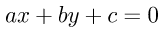
，轉為矩陣表示
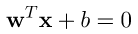，那麼我們只要求出點到藍色線條的最短距離即是margin。除此之外別忘記我們的問題是要分類，也就是說有一類對應的公式為
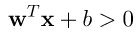和另一類為
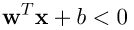，那麼將兩個式子乘上對應的label，及合併為
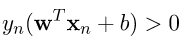，接著我們要嘗試一步一步慢慢的解出距離公式。
要如何求出距離?實際上就是計算投影長度，簡單複習投影公式如下圖二，投影的公式是很容易推導的，相信大家公式一出來就能夠馬上回想起來，這裡我們舉個簡單的例子，假設v=(4, 3)，u=(5, 10)，那麼u_v的長度帶入公式計算出來為10。所以總結來說u在v方向做投影的長度為10。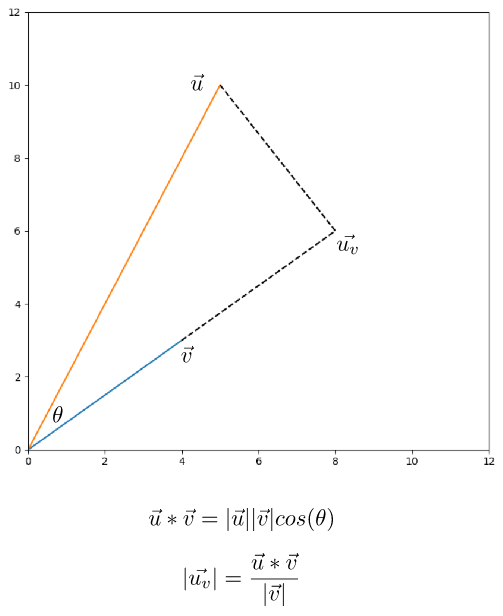
圖二。
接下來考慮一個點到一個平面上做投影，如圖三，灰色為切割平面，x'和x''和w垂直，也就是法向量，那麼要計算x到平面距離就簡單了，上述的投影公式帶入，x對w方向做投影，u=(x - x')，v=w，就能計算距離，如圖四，灰色為垂直到w的向量，紅色為長度。
註：u=(x - x')，能想像是將x'設為起始點，以上述投影公式為例，也就是說我們剛剛計算的起始點是(0, 0)，因此可以忽略，若是(4, 3)為起始點則長度則變為5。
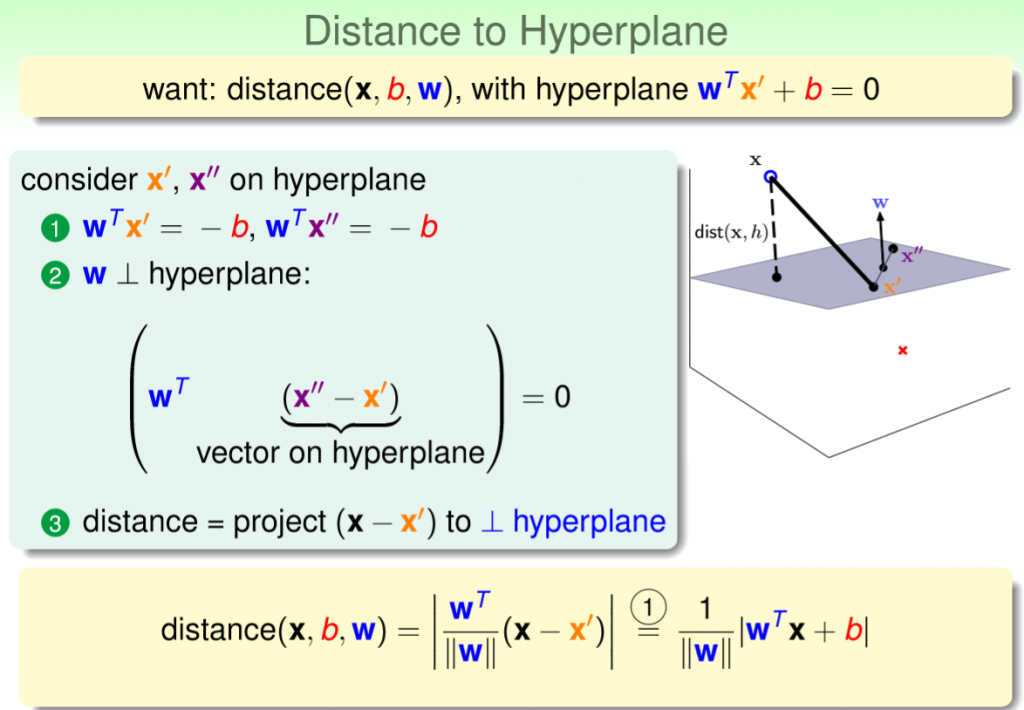
圖三，來源[1]。
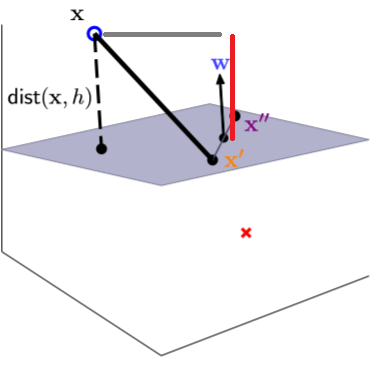
圖四，來源[1]。
現在我們能夠利用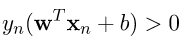的條件，將剛剛推導出來的公式的絕對值拿掉，轉為
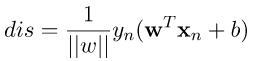，現在我們整理一下剛剛到現在的公式和條件。詳細如圖五。
1.我們要找到最佳參數使得margin最大化。
2.每一筆資料計算出來的方程式乘上對應的label必須大於0。
3.margin算出來的結果，即是所有資料中最小得距離。
圖五，來源[1]。
實際上沒有這麼多條線，都僅僅只是縮放倍率不同，因此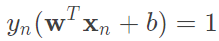
所求得的結果是一樣的，而這對我們的好處就是能將原先要最大化的式子轉為，
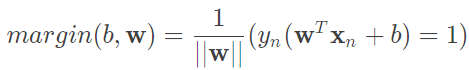，使得我們最大化更加簡易，詳細如圖六。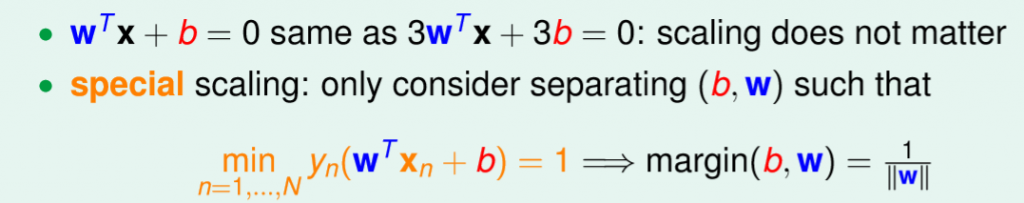
圖六，來源[1]。
現在固定住每一筆資料計算出來的方程式乘上對應的label的結果，因此現在我們整體公式則轉為圖七，整個公式和條件如下。
1.我們要找到最佳參數使得margin最大化。
2.每一筆資料計算出來的方程式乘上對應的label的結果，最小的必須等於1。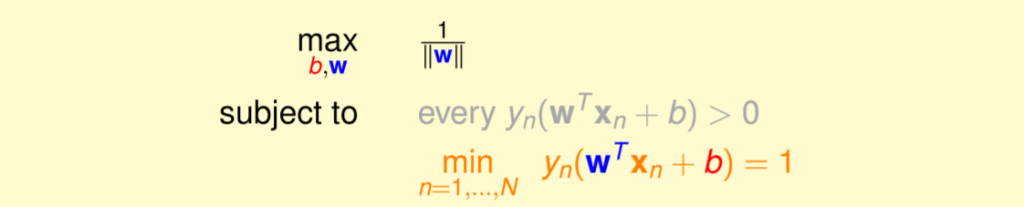
圖七，來源[1]。
很顯然除了最大化以外，我們還要計算最小化條件，所以我們希望條件放寬鬆一點。原先我們要最小化等於1，也就是說每一個計算的結果都是大於等於1，現在我們有一個更寬鬆的條件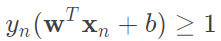
。有了這個寬鬆條件之後，我們必須去證明這個轉換是否會改變原先優化目標。
考慮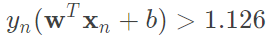
，那麼
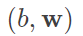的最佳化為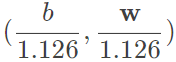
，由除以大於1的值，可得知b和w的長度縮小了，但原先我們在最大化的就是
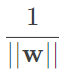，也就是最小化
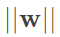，然而剛剛算出來的結果代表著更小的b和w，很顯然是不成立的，因此可以說轉為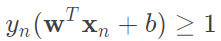是不會改變整個優化的結果。
圖八，來源[1]。
通常在解最佳化問題時，我們習慣最小化參數，因此取倒數，而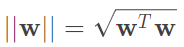
，因此我們對
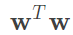求最小化是相同的，那這裡還會除2，事實上這些過程是為了要滿足二次規劃性質所做的簡化。詳細如圖九。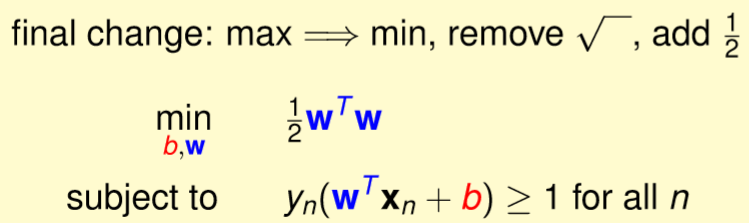
圖九，來源[1]。
上述提到我們就是在簡化為符合二次規劃的性質，而二次規劃就是一個最佳化問題，並且已有對應的解法，我們能使用凸優化的套件達成，現在我們要將剛剛簡化的式子對應到二次規劃的公式即可。詳細如圖十。
圖十，來源[1]。
現在我們有相對應的公式，那就能夠實作出簡易版的SVM，這裡凸優化套件使用cvxopt，並且依照官方文件說明來去對應到剛剛所推導的公式。如圖十一。
註:需卸載numpy安裝numpy+mkl。
圖十一，來源[2]。
公式
將x向量都補上一個b，也就是b_x向量。
條件
參數
設u=二次規劃的解(x)，則w = u[1:]，b = u[0]，margin=1 / ||w||。
support_vectors=min(m * x + b)，也就是找到最小的margin，實際上對於二次規劃的最大化的z條件為大於等於0如圖十二，因為A這裡無使用到和q=0，所以計算結果由G(對應投影片的A)和z控制，而z跟G(對應投影片的A)的關西就變為，若z=0則無影響，若z>0則有影響，因此可由z得知，若z大於0，代表是support_vectors，因為只有support_vectors才會影響margin。(可跳過，後面不會使用z得到support_vectors)。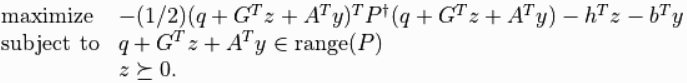
圖十二，來源[2]。
def fit(self, x, y):
'''
SVM formula:
optimal(b, w)
min 1/2 * w^T * w
subject to y_n(w^T * x_n + b) >= 1
Quadratic Programming:
optimal u←QP(Q, p, A, c)
min 1/2 * u^T * Q * u + p^T * u
subject to a_m^T * u >= c_m
objective function:
u = [b, w]^T
Q = [[0, 0_d^T],
[0_d, I_d]]
p = 0_(d + 1)
constraints:
a_n^T = y_n[1, x_n^T]
c_n = 1
M = N
Correspondence cvxopt op:
P = Q
q = p
G = A
h = c
x = u
'''
assert ((len(x) == len(y))), "size error"
assert ((len(x) == len(y)) & (len(x) > 0)), "input x error"
x_len = len(x)
b_x = np.concatenate([np.ones((x_len, 1)), x], axis=-1)
dimension = len(b_x[0])
eye_process = np.eye(dimension)
eye_process[0][0] = 0
Q = cvxopt.matrix(eye_process)
p = cvxopt.matrix(np.zeros(dimension))
A = cvxopt.matrix(np.reshape(y, (-1, 1)) * b_x * -1)
c = cvxopt.matrix(np.ones(x_len) * -1)
cvxopt.solvers.options['show_progress'] = False
result = cvxopt.solvers.qp(Q, p, A, c)
u = np.array(result['x'])
self.__alphas = np.array(result['z']).flatten()
self.__sv = self.__alphas > 1e-6
self.__w = u[1:].flatten()
self.__b = u[0]
self.__support_vectors = x[self.__sv,:]
'''
Vertical dist:
|(ax + by + c)| / sqrt(a^2 + b^2)
'''
self.__margin = 1. / np.linalg.norm(self.__w)
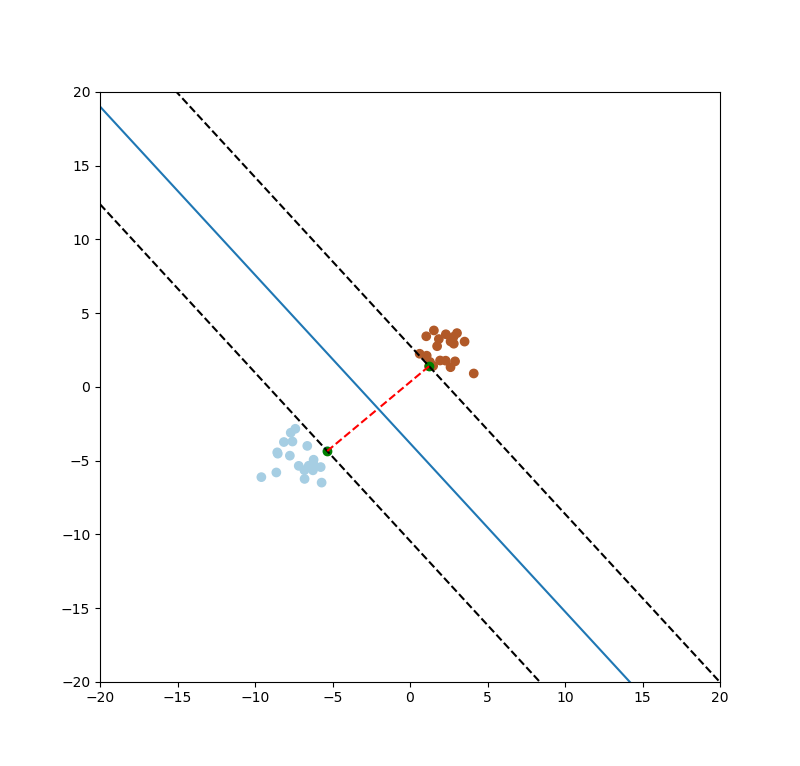
圖十三。
上述介紹的SVM是基於線性空間中所推導的，那現在我們想解決一個非線性問題就必須將x向量轉換至非線性空間中，如圖十四，而我們的維度從d轉至d'，這時候就產生一個問題，假設d'越大，剛剛我們所要解的二次規劃問題的參數也就越多，這意味著d'趨近於無限大，參數也就趨近於無限大。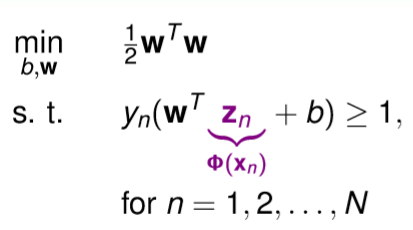
圖十四，來源[1]。
我們要如何解決這個棘手的問題?我們可以將原先式子要從d個維度解轉為另一個式子從N筆資料去解，如圖十五。
圖十五，來源[1]。
如何做到這件事?相信有些朋友在介紹Linear SVM時已經會有疑問是不是能將條件使用拉格朗日乘數將條件加入式子，這裡的確第一步將剛剛的條件使用拉格朗日乘數做轉換，轉換後如圖十六，比較不同的地方是這裡將lambda換為alpha，但這並不影響我們去解析。
註:拉格朗日乘數能想為正則化的概念(實際上有數學證明)，類似今天給定一個圓的大小(有上下限)，我希望在這個圓的大小內求得最好的解。而SVM主要是限制原先的條件，假設條件式z >= 1(無上限)，也就是說我們希望z最小(下限)就是等於1，lambda(z - 1)，使用lambda來控制這個條件我們要看得多重，也就是我整個式子z大於1的權重。
圖十六，來源[1]。
林軒田教授更直接的使用公式讓讀者能更容易理解為何拉格朗日乘數這樣做是合理的，首先固定b和w，紅色框框代表b和w的式子(原先的式子)。
假設b和w是差的，也就是說b和w沒達到min，裡面的項越大意味著會接近無限，理所當然結果也是無限。
假設b和w是好的，也就是說min到最小化，意味著拉格朗日乘數的式子會等於0(alpha>=0，裡面的式子也是大於等於0)，換句話說alpha_n或裡面的式子會等於0(先不考慮兩個都0)，最後得到的結果就是原先的式子。
圖十七，來源[1]。
假設alpha'是固定的，那我們可以得到以下式子，如圖十八，因為左式alpha是最大化，那右式alpha'所計算出來的結果就會小於等於左式。(由上述能得知右式最小就是等於0，若還沒等於0固定代表著它可能大於等於0)。
圖十八，來源[1]。
那我們再將右式的alpha'求最大化也會比左式還要來的小，能想為我們能肯定左邊的alpha是最大化的參數，那麼將右式alpha'最大化參數後的結果，最多也只會等於左式的結果，所轉換後的式子也就是所謂的對偶問題(最大化變最小化，最小化變最大化)。
這對我們有甚麼好處?原先我們要先max有條件的alpha式子，但現在能先優化沒有條件的min式子，這意味著我們可以先簡化min內的參數，也就是先求偏微分。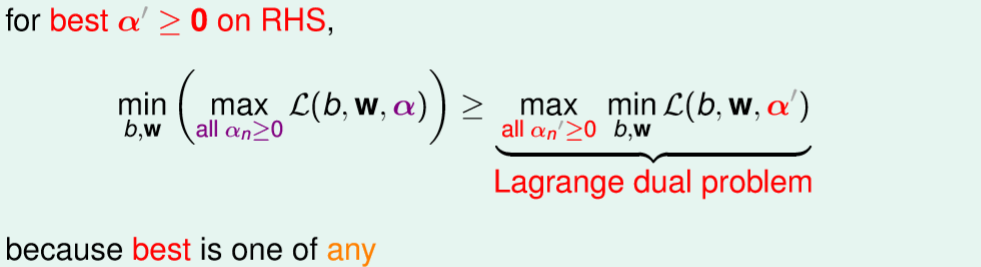
圖十九，來源[1]。
上述的對偶的問題，稱為弱對偶，若是等於則是強對偶，在二次規劃中，若我們滿足某些條件則對偶式子就能說是強對偶，如下圖二十，而恰好我們在解的問題都滿足這些條件，詳細如下。
1.問題是凸函數。
2.原始的問題是有解的，在這裡也就是我們想要找的分割平面。
3.是線性的條件。
圖二十，來源[1]。
對b和w兩個做偏微分找到最小化的參數所要滿足的條件，這裡只需計算偏微分即可得到結果，詳細如圖二一。
圖二一，來源[1]。
帶入上述式子，可以將min拿掉，加入推導後的條件，這與解原先式子是相同的，詳細如圖二二。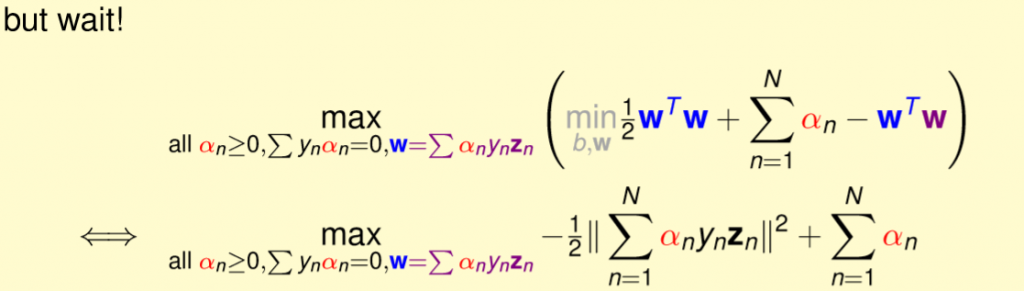
圖二二，來源[1]。
整理一下剛剛到現在的公式和條件，如下圖二三，這通常我們都稱為KKT的條件。
圖二三，來源[1]。
上述推導的結果相同的都是為了滿足二次規劃，先將原式展開，一樣轉為二次規劃的公式，詳細如圖二四。
在程式中可能會有稍微不同，這裡使用矩陣來去表達sum的式子，假設我有40筆資料，則y大小=(40, 1)，z大小(40, N)，那alpha大小為(40, 1)。
1.yn * ym使用矩陣表示為，y和自己的轉至矩陣相乘，矩陣大小變為dot((40, 1) * (1, 40))=(40, 40)。
2.zn * zm使用矩陣表示為，z和自己的轉至矩陣相乘，矩陣大小變為dot((40, N) * (N, 40))=(40, 40)。
3.再將兩個做點積dot(y * y^T) * dot(x * x^T)也就是yn * ym * zn * zm = Q，矩陣大小(40, 40) * (40, 40) = (40, 40)。
4.原本應該再乘上alpha的矩陣相乘alpha * alpha^T，但為了滿足二次規劃的矩陣相乘，先與第一項alpha^T矩陣相乘Q，矩陣大小變為dot((1, 40) * (40, 40)) = (1, 40)。
5.最後和alpha矩陣相乘，矩陣大小變為dot((1, 40) * (40, 1)) = (1)，若還是太抽象能將符號帶入整個展開，結果一樣是會得到原始的sum的式子。
圖二四，來源[1]。
公式
條件
參數
w：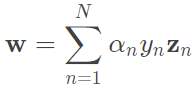
support_vectors：只找到alpha大於0(趨近於0, 1e-5...)的值就是support_vectors，因為會使得裡面的式子等於0，所以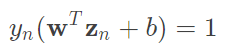
，這式子代表的就是這個點剛好在margin的邊界上，也就是最原始的條件=1，只是為了方便將其推導後變成>=1(若忘記能往回看推導)，上述這些隱藏著一個資訊，實際上如果再邊界上計算結果會等於1，也就是說真正控制margin的只有在邊界上的點，而這個點就是support_vectors。
b：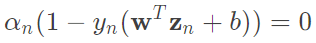
得知若alpha大於0則推出
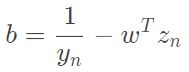，只有support_vectors的alpha不等於0，因此使用support_vectors就能夠算出b這個截距，程式碼中只拿一個support_vector計算，因此dot跟點積一樣(一維)，當然也能計算全部再平均，但在這裡沒有太大的誤差，因此直接拿任一個support_vector來計算。
def fit(self, x, y):
'''
SVM formula:
optimal(b, w)
min 1/2 * sum_n(sum_m(a_n * a_m * y_n * y_m * z_n^T * z_m)) - sum_n(a_n)
subject to sum_n(y_n(a_n)) = 0
(a_n) >= 0
Quadratic Programming:
optimal a←QP(Q, p, A, c)←QP(Q, p, A, c, B, b)
min 1/2 * a^T * Q * a + p^T * a
subject to a_m^T * u >= c_m
objective function:
Q = y_n * y_m * z_n^T * z_m
p = -1_N
A and c are N conditions
B and b are a condition
constraints:
A = n-th unit direction
c = 0
B = 1_n
b = 0
M = N = data size
Correspondence cvxopt op:
P = Q
q = p
G = A
h = c
B = A
a = u
'''
assert ((len(x) == len(y))), "size error"
assert ((len(x) == len(y)) & (len(x) > 0)), "input x error"
x_len = len(x)
dimension = len(x[0])
y = np.reshape(y, (-1, 1))
Q = cvxopt.matrix(np.dot(y, y.T) * np.dot(x, np.transpose(x)))
p = cvxopt.matrix(-np.ones(x_len))
A = cvxopt.matrix(-np.eye(x_len))
c = cvxopt.matrix(np.zeros(x_len))
B = cvxopt.matrix(np.reshape(y, (1, -1)))
b = cvxopt.matrix(np.zeros(1))
cvxopt.solvers.options['show_progress'] = False
result = cvxopt.solvers.qp(Q, p, A, c, B, b)
self.__alphas = np.array(result['x']).flatten()
self.__sv = self.__alphas > 1e-6
self.__w = np.sum(np.array(result['x'] * y * x), axis=0).reshape(-1)
self.__support_vectors = x[self.__sv,:]
self.__b = (1./ y[self.__sv][0]) - np.dot(self.__w, x[self.__sv, :][0])
#self.__b = ((1./ y[self.__sv])
# - np.sum(
# self.__w.reshape(-1,1).T * x[self.__sv, :],
# axis=-1,
# keepdims=True)
# )[0]
'''
Vertical dist:
|(ax + by + c)| / sqrt(a^2 + b^2)
'''
self.__margin = 1. / np.linalg.norm(self.__w)
圖二五。
再上一個小章節，我們提到將z當作是x的一個轉換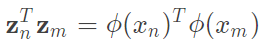
，然而這樣我們計算量會增加，因為轉換要計算一次，轉換完後還要計算一次內積，因此這裡想要解決的問題是，我們希望通過一個式子能夠一次轉換和內積，而這式子也就是所謂的kernel。詳細如下圖二六。
圖二六，來源[1]。
首先考慮一個多項式，這裡以二項次為例，如下圖，並且式子內的x1x2和x2x1這兩者結果是一樣的(原先會寫為2 * x1x2)，整個展開這對我們後面簡化是有幫助的。
圖二七，來源[1]。
假設x和x'兩個轉換再做內積，如圖圖二八，等於零次項+一次項+二次項，將二次項拆分為i和j，最後發現我們只需要計算x和x'的內積就能夠解出轉換+內積，在這裡代表著O(n^2)變為O(n)。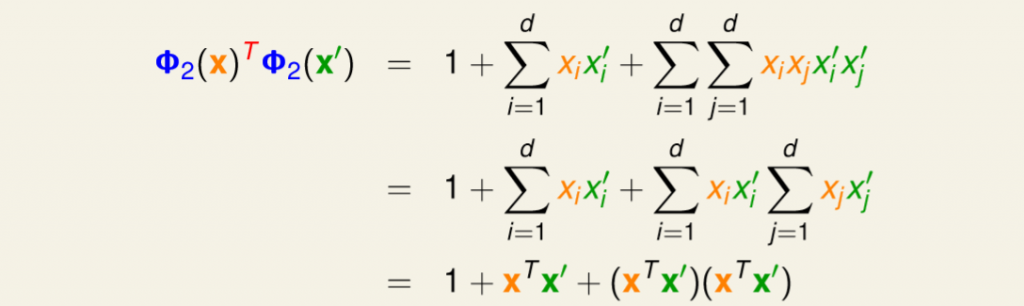
圖二八，來源[1]。
上述的二次轉換我們使用一個符號來代替，公式為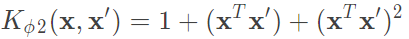
，則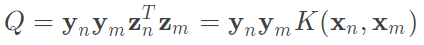
，接著我們還需要解與原始z有關的參數，包含w、b、預測，實際上w會變為一個中間產物，最後都會轉為kernel，所以首先考慮b如何變為kernel的形式。詳細如圖二九。
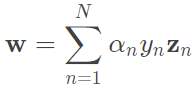，將b原始式子的w換為上述公式，則等於與support vectors做內積，那最後那一項就可以換為
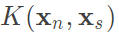，這樣b就能夠使用kernel取得。
圖二九，來源[1]。
整理上述整個步驟，詳細如圖三十。
我們是不是能將Polynomial Kernel改為比較通用的形式，而不是只侷限在於剛剛的式子，詳細如圖三一。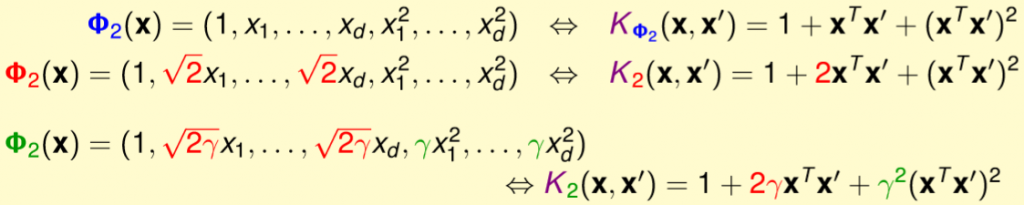
圖三一，來源[1]。
上述很明顯告訴我們，通用式能寫成一般的(1 + ax)^2，如下圖。(參數影響自行測試)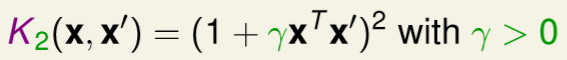
圖三二，來源[1]。
相信有些人也已經想到是不是能將1和次方項都設定為參數，的確可以，如下圖。(參數影響自行測試)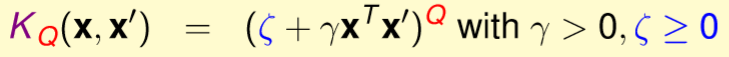
圖三三，來源[1]。
參數
kernel_x：帶入公式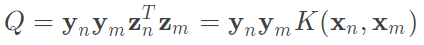，，對自己每一個做內積，也就是自己和自己的轉置做矩陣相乘。
b：帶入公式，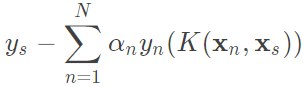
，先行將所有的y_sv做總和再檢掉後項，而只需要計算alphas > 0的值也就是support vectors(其它=0，怎麼算都是0)，這裡alphas和y要先轉為(N, 1)也就是N個support vectors的數量在做點積，最後再和K(x_sv, x)轉換kernel做點積，總和後做平均就是b。(若alphas和y轉為(1, -1)，則polynomial_kernel的x0和x1互換即可，這是矩陣的特性，用行算或用列算都能)。
def polynomial_kernel(x0, x1, zeta=1., gamma=1., Q=2):
assert zeta >= 0, "zeta error"
assert gamma > 0, "gamma error"
return (zeta + gamma * np.dot(x0, np.transpose(x1))) ** Q
kernel_x = polynomial_kernel(x, x, self.zeta, self.gamma, self.Q)
Q = cvxopt.matrix(np.dot(y, y.T) * kernel_x)
self.__a_y = np.reshape(self.__alphas[self.__sv], (-1, 1)) * np.reshape(y[self.__sv], (-1, 1))
self.__b = np.sum(y[self.__sv])
self.__b -= np.sum(self.__a_y * polynomial_kernel(self.__support_vectors, x[self.__sv], self.zeta, self.gamma, self.Q))
self.__b /= len(self.__support_vectors)
我們能不能轉換到一個更多維甚至無限維度的空間?事實上Gaussian Kernel能做到這件事，如圖三四，假設有兩個變量x和x'。
上述我們使用一個變量來表示高斯，若有影像處理基礎的應該知道，任何維度的高斯都會經過正規化，若不做正規化，當維度越高值就越大，則計算出來的結果也會越大甚至溢位。那在這裡將上述變量推廣到多維，則就是多了一個計算正則化，也就是L2範數，如下圖。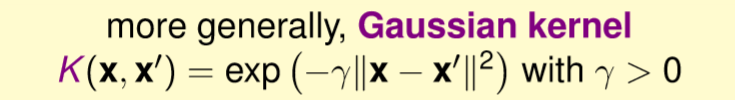
圖三五，來源[1]。
只需要改變kernel轉換函數就能夠使用
def gaussian_kernel(x0, x1, gamma=1.):
assert gamma > 0, "gamma error"
return np.exp(-gamma * np.linalg.norm(np.expand_dims(x0, axis=1) - x1, axis=-1) ** 2)
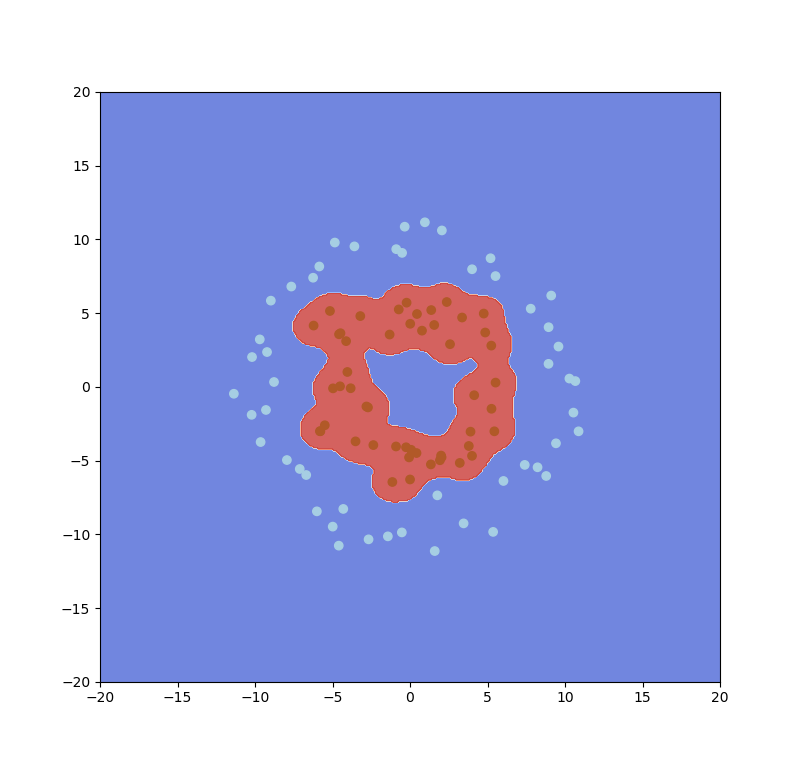
Linear Kernel：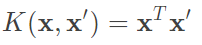
優點：不用經過轉換和條參所以完成速度快，因此有些問題可以先嘗試用linear kernel去解決，另外解出來的w跟平常的線性方程式一樣，因此也較容易解釋。
缺點：只能做線性分割，那也有人使用線性分割做權重變為能解決非線性分割的問題，像是之前介紹的AdaBoost。
Polynomial Kernel：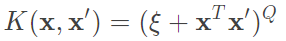
優點：條件比Linear寬鬆，簡單來說比Linear更能解決非線線問題，能調控Q來決定轉換的空間。
缺點：因為次方關西，當裡面式子小於0，次方越大值就會越小(趨近於0)，裡面式子大於0，次方越大值就會越大(溢位)，這兩者都是多向式的缺點，另外要調整的參數量也相對的多。
Gaussian Kernel：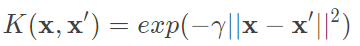
優點：相較於上述kernel，Gaussian的無限維度能表現出更複雜的函數，而他的上下限是0~1之間，因此也比poly還要穩定，需要調整的參數僅僅只有一個。
缺點：訓練出來的w很難去解釋，因為我們是轉換到無限維度進行處理，很難去解釋一個無限多維分類的空間，而計算速度相對linear也慢了許多，另外參數部分若設置不佳則很容易達到overfitting。
上述介紹的所有方法結果是每個資料都必須分對，然而這很可能導致overfitting或者資料代表性不夠導致測試資料的準確率低，如下圖三六，A圖允許了一些錯誤，B圖全部都分類對，但A圖的分割可能比B圖還要好，對margin而言，A圖我們稱為soft margin，B圖則是hard margin。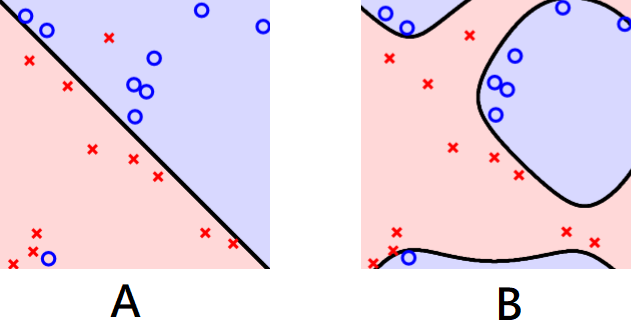
圖三六，來源[1]。
我們要如何做到容許一些錯誤呢?回想我們原始min的式子為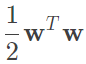
，那我要容許錯誤，也就是預測不等於y，那代表著違反條件，所以與它對應的條件為大於等於-inf，那現在我們的式子就要變成要找到一個最小的margin加上最小的錯誤，C則是在控制兩者的比例，詳細如下圖。
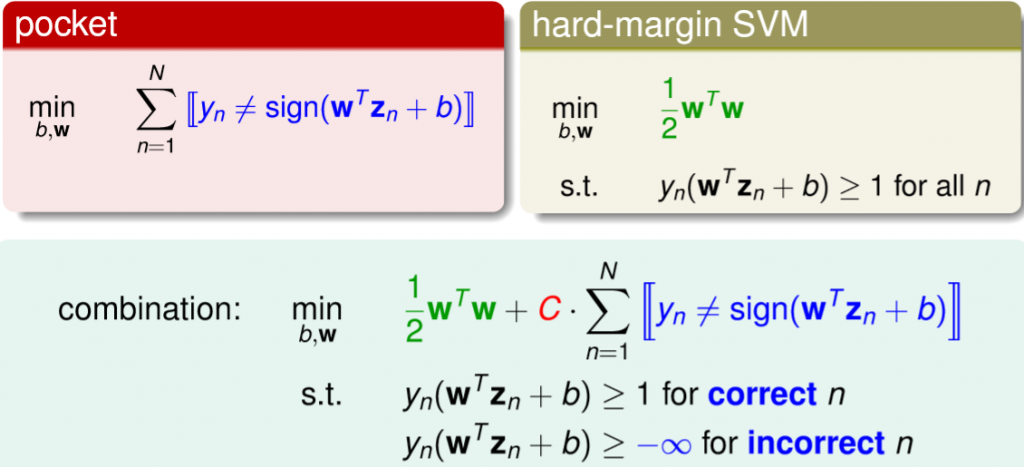
圖三七，來源[1]。
整理一下式子，將兩個條件合併，分對的就會>=1，分錯的就會>=-inf，合併起來如下圖公式。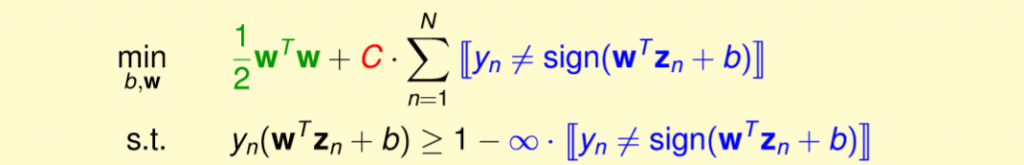
圖三八，來源[1]。
很明顯上述問題是非線性,我們就無法使用二次規畫解決，因此我們將問題轉為下列公式，用一個符號代表每一個分類的小錯誤或大錯誤(與先前的AdaBoost很相似)，這也就是soft margin SVM的一般式。
圖三九，來源[1]。
對偶公式一樣跟上述相同，都先用拉格朗日乘數將條件帶入，再找到lower bound，經過特定條件轉為強對偶，公式如下圖。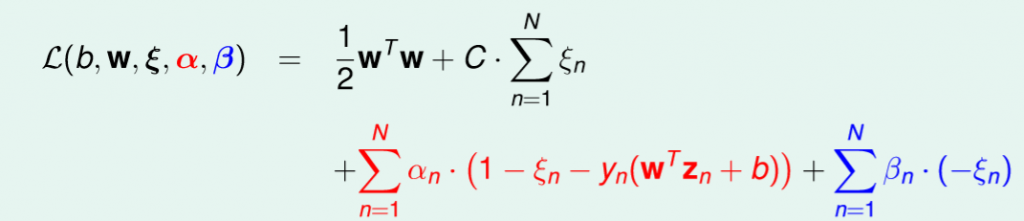
圖四十，來源[1]。
相同的先對裡面的式子做偏微分做簡化如下，比較不同的是經由偏微分得到soft margin只要約束alpha的範圍值就能夠不用多計算另一個條件的beta。詳細在往下看公式整理。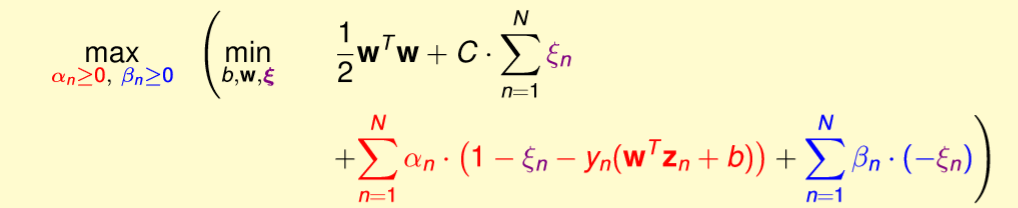
圖四一，來源[1]。
圖四二，來源[1]。
整理後的公式如下圖，能觀察到與原本相比只有alpha多了一個範圍條件，而這也就是soft margin SVM。
圖四三，來源[1]。
還有一個參數是我們使用條件反推回去的，就是b(截距)，原始公式為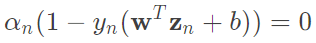，那現在這個條件還多了一個xi這個參數，因此就必須使用現在這個條件做推導，但要計算出xi就必須計算出b，計算出b就必須計算出xi，那要如何解決這問題?我們只要使得xi=0，就能夠跟原始式子一樣計算，那可以使用偏微分求出的alpha和C來推出alpha若小於C則xi=0，因此若滿足0 < alpha < C則就能夠計算b，通常我們稱它為free support vectors(有極少數有例外，也就是沒有小於C的support vector，這裡先忽略)。詳細如下圖。
圖四四，來源[1]。
我們能依照推導出的公式給出三種可能，並分析三種可能的特性對其分析，如下圖四五。
只需要多入加alpha的條件，和b的計算從sv變為free_sv。
A = cvxopt.matrix(np.concatenate([-np.eye(x_len), np.eye(x_len)]))
c = cvxopt.matrix(np.concatenate([np.zeros(x_len), np.ones(x_len) * self.C]))
self.__free_sv = (self.__alphas > 1e-6) & (self.__alphas < self.C)
self.__free_support_vectors = x[self.__free_sv,:]
self.__free_a_y = np.reshape(self.__alphas[self.__free_sv], (-1, 1)) * np.reshape(y[self.__free_sv], (-1, 1))
self.__b = np.sum(y[self.__free_sv])
self.__b -= np.sum(self.__free_a_y * gaussian_kernel(self.__free_support_vectors, x[self.__free_sv], self.gamma))
self.__b /= len(self.__free_support_vectors)
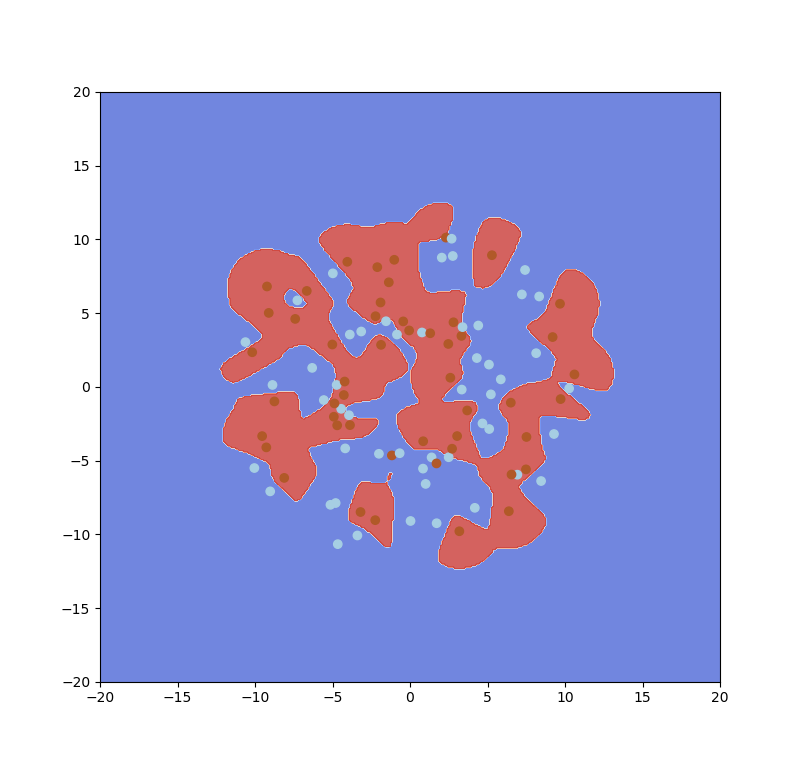
將不同的C和gamma進行交叉驗證如圖四六，每次計算xi或accuracy，最後做平均，如圖四七。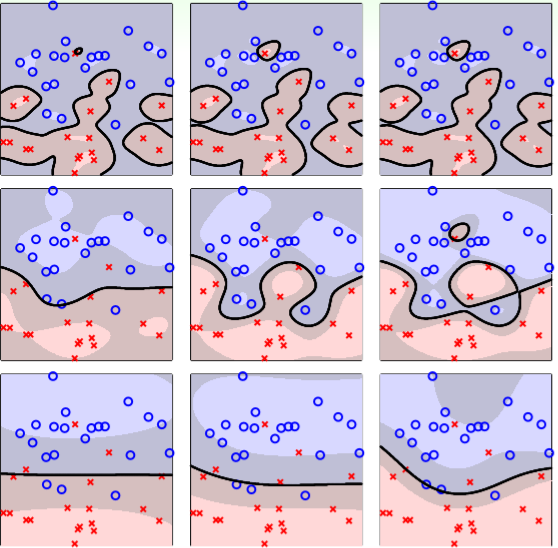
圖四六，來源[1]。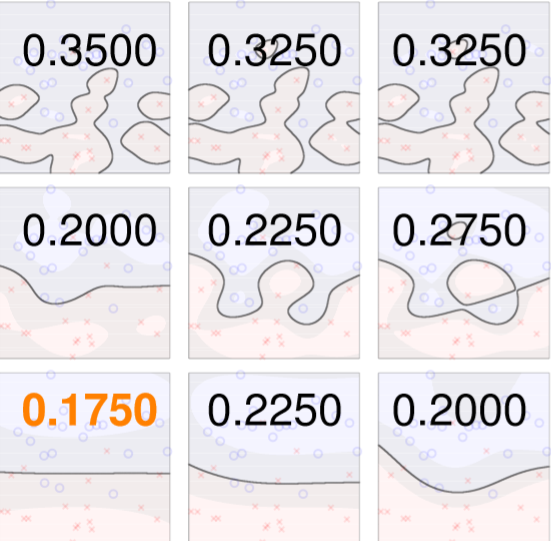
圖四七，來源[1]。
和CV很像，只是將每筆資料都視為一個fold，也就是說我有N筆資料就有N個fold，最後將全部fold預測結果結合起來做評估，那再SVM有一個特性，Error的數量絕對會小於等於Support Vectors的數量，事實上這很直觀，先前我們說過只有support vectors才會影響邊界，也就是說如果Leave-one-out非margin的點則margin還會是相同的，所以準確率不變，若Leave-one-out是margin上的點並且分錯，最多也只會有support vectors的數量會分錯。
林軒田教授用了更容易明白的例子，如下圖，假設我們有10000個點，那麼代表我們有10000個最佳化參數alpha，若我們拿掉一個不是support vector的點，則剩下的9999個alpha還是最佳解，因為不是support vector代表alpha=0，所以一定也一樣是最佳解，那麼我們能說有無拿掉的結果所影響的error都是0，若是support vector則是小於等於1，因此能說錯誤的數量小於support vectors的數量。
圖四八，來源[1]。
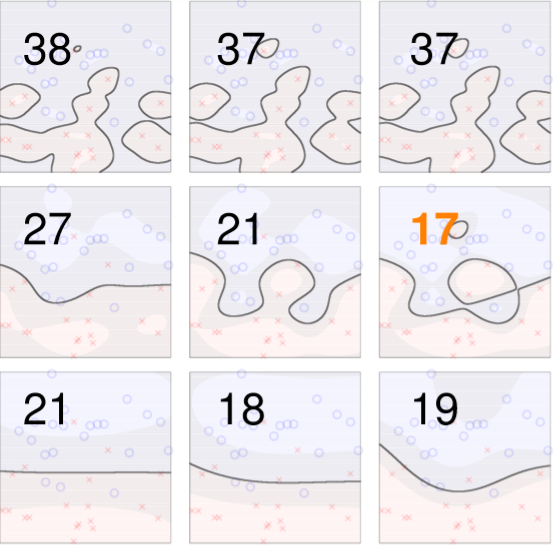
圖四九，來源[1]。
在學習過程中對於SVM的方法和評估更加了解，也要感謝有這些人的付出才能讓我們能夠更快速的學到這些精華，對於現在的SVM來說選擇好的參數是一個重點，而在許多研究當中也有深度學習結合SVM的例子，像是使用深度學習得取embedding(hight-level feature)，進而再使用SVM分類，事實上我們也能朝著這個方向思考，如何做few-shot learning，這個問題若未來有機會，會做更詳細解說，若以上有問題或有侵權可留言或私訊聯絡。
[1] Hsuan-Tien Lin > MOOCs, [Online]. Available: https://www.csie.ntu.edu.tw/~htlin/mooc/ [Accessed: May. 31, 2020]
[2] Cone Programming — CVXOPT User's Guide, [Online]. Available: https://cvxopt.org/userguide/coneprog.html [Accessed: May. 31, 2020]
您好，請問只要是預測，不管是用迴歸 隨機森林 SVM，都是需要先有新資料的自變數X，才能預測應變數Y嗎?
對的，因為在訓練時也是給定一個X輸出一個Y，廣域一點來說這些方法都是屬於監督式的模型，因此能解釋這些模型在做X轉換到對應Y。
了解，謝謝您~
iThome鐵人賽
看影片追技術